Wave Power

Wave power is important because as waves generate more power, they have a greater capacity for eroding the shoreline.  From the CEE 514 class notes, the total wave power can be calculated by first finding the wave energy density using the following equation:

E = 1/8*ρ*g*H²

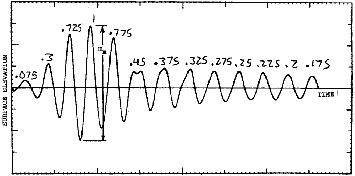
where ρ = 1000 kg/m³ and g = 9.81 m/s².  When boats produce a wake, they create more than just one wave.  Sorensen estimated that boats create 13 measurable waves of different amplitudes as shown in the figure below.

Therefore, to find the total wave energy produced by one passing boat, we must sum up all the energies resulting from each wave in the figure. Then we must multiply that amount by the number of passing boats per day.  I will assume that there are an average of 5 boats on Ada Lake each day and each boat will travel around the lake 15 times per day. 

Similarly, since the wind speed being used is a long term average, we will assume that the wind is blowing all day long, resulting in 24 hours of waves.  The wave energy calculated per wave must then be multiplied by 86,400 seconds since the period of the waves is about 1 second.

Wave power, calculated by dividing the wave energy by the wave period (assuming shallow water), is shown in the graph below.  This graph is only for boats at a distance of 30.48 m (100 ft) from the shore, but the graphs for other distances will look similar.

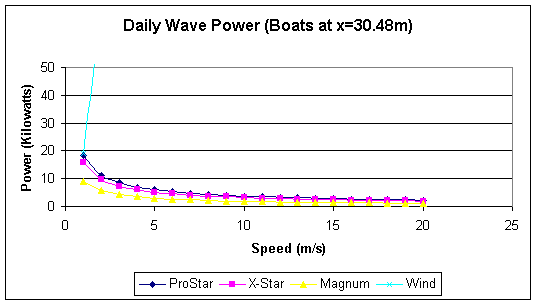
Note: The wave power due to wind is only visible for speeds less than two because of the scale of the graph.  The power produced from wind is orders of magnitude greater than the power produced from boats.

Wave Height           Wave Power           Sediment Resuspension