Introduction to FEMSEICHE
Applicability
Methodology
Required Data
Further
Information
Introduction to FEMSEICHE
FEMSEICHE is a MATLAB script that was written by Rueda and Schladow
(2002) for computing both the periods and the spatial
variation free modes of seiches in basins with any arbitrary shapes.
Applicability
FEMISEICH can be applied to any basins of small to medium size where
the coriolis effect can be neglected. To determine of the importance
of the rotation effects on a basin, we can use Rossby radius of
deformation, which describes the relationship between the coriolis
force and the pressure gradient force.
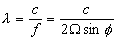
|
¡@ |
where |
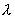 |
= |
Rossby radius
of deformation |
|
¡@ |
¡@ |
c |
= |
gravity wave
propagation velocity =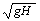 |
|
¡@ |
¡@ |
g |
= |
Gravitational
acceleration |
|
¡@ |
¡@ |
H |
= |
Water depth |
|
¡@ |
¡@ |
f |
= |
Coriolis
parameter = 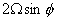 |
|
¡@ |
¡@ |
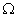 |
= |
Angular velocity
of rotation of the Earth |
|
¡@ |
¡@ |
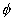 |
= |
latitude |
FEMISEICHE can be applicable when the Rossby radius
of deformation of one basin is much larger than the basin width.
¡@
Methodology
Periods
of seiches are functions of the lake geometry, water level
fluctuations and coriolis effects and FEMSEICHE tried to simply the
problem by:
(1)
neglecting the coriolis effects
(2)
neglecting
friction
(3) assuming amplitudes of seiches are small
Based on the
above assumptions, an equation describing the periods of seiches and
the "spatial structure" of the free modes of seiches can be derived from continuity and conservation
of momentum:
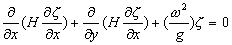
| ¡@ |
where |
H |
= |
spatially
varying basin depth |
| ¡@ |
¡@ |
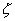 |
= |
free surface
displacement from an equilibrium position |
| ¡@ |
¡@ |
x,y |
= |
coordinates
of nodes in the horizontal plane |
The equation can be solved together
with a boundary condition which describe no flow takes place across
the boundaries of the basin.
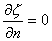
| ¡@ |
where |
n |
= |
normal direction |
FEMSEICHE solves the 2 above
differential equations to identify the "spatial structure" of seiches
using the finite element method. Based on the "spatial structure" of
seiches, FEMSEICHE then computes the associated velocity field using
the linear frictionless depth-averaged shallow water equations, which
in turns gives the periods of seiches.
¡@
Required
Data
3 sets of data are required
| ¡@ |
(1) |
geographic location
|
| ¡@ |
¡@ |
which lists the
numbering of
data points, x and y coordinates and depth at each data point |
| ¡@ |
(2) |
finite element mesh |
| ¡@ |
¡@ |
which lists
the linkage of data points into triangles in the counterclockwise
direction (see the example shown below). The triangular mesh can
either be generated by hand or by computer programs. |
| ¡@ |
(3) |
water level |
| ¡@ |

Example
number
of triangle node1 node2 node3
1
1 4
5
2
1 5
2
¡@ ¡@ |
¡@
Further information
Further information on FEMSEICHE can be found at the webpage developed
by Rueda, one
of the developers of FEMSEICHE (http://my.engr.ucdavis.edu/~edllab/Users/Rueda/femseiche.html)
where you can also find the MATLAB script of FEMSEICHE and an example.
¡@ ¡@ ¡@ |
