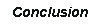Conclusion

Theoretical Significant Wave Height and Period (using the SMB method):

Low Wind Speed

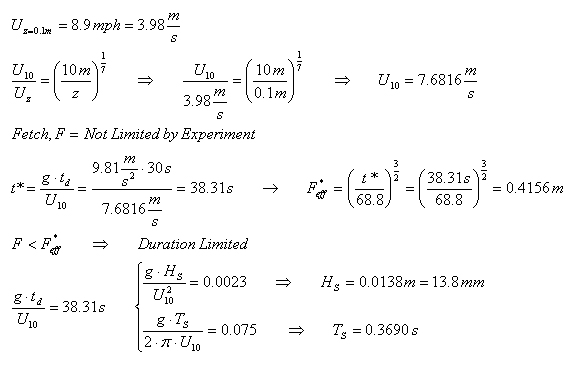
High Wind Speed

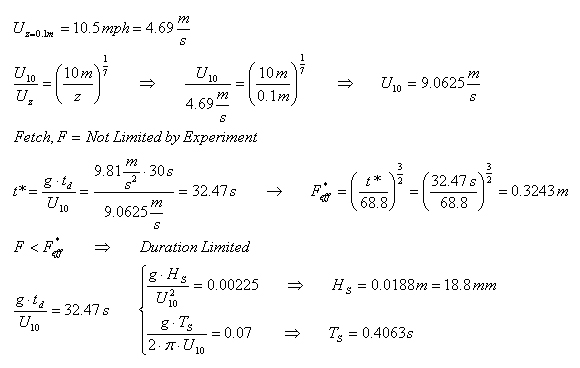
 Summary of Experimental Results:

Low Wind Speed

High Wind Speed

Analysis of Experiment:

Wave Height:

The theoretical models suggest that wave height should grow until it reaches the fully developed state.  From the plots of the Significant Wave Height, it can be seen that the wave height do in fact experience growth.  The first significant wave height (at the 10 cm wave gage) appears to be an outlier because it does not agree with the rest of the data points.  The theoretical calculations suggest that the effective fetch is 41.56 cm for the low wind speed and 32.43 cm for the high wind speed.  The plots show that the experimental results are consistent with the theoretical calculations, in that the peaks of the significant wave heights occur right around 40 cm with the peak for the low wind speed occurring at a slightly farther distance from the fan (occurring at about 41 cm) then that of the high wind speed (occurring at about 39 cm).  Beyond the effective fetch, the waves have reached their maximum wave height (duration limited), and the wave heights diminish due to the frictional forces between water molecules.  The theoretical calculations suggest that the significant wave height for the low wind speed should be 13.8 mm and for the high wind speed it should be 18.8 mm.  Theoretically, these values should match up with the peak significant wave heights from the plots, approximately 6.3 mm for the low wind speed and 10 mm for the high wind speed.  From this we can see that the experimentally determined values do not match the theoretical values.  However, the trends that the theoretical calculations suggest do match the experimental date, in that wave height is directly proportional to wind speed.

Wave Period:

The theoretical models suggest that wave period should increase as waves grow into fully developed waves.  Unfortunately the wave period plots of experimental data came out scattered and do not show any definite trends.  If the second data point (the 25 cm wave gage) for the low wind speed plot is considered to be an outlier, the data would in fact follow the trends that are suggested by the theoretical models.  In other words, the plot would show that the wave period increases over the effective fetch (about 50 cm), where it would then reach its maximum (0.13 seconds) and diminish after that.  The theoretical calculations suggest that the wave periods should be 0.3690 sec for the low wind speed and 0.4063 sec for the high wind speeds.  These values are obviously much higher then the maximum wave periods that were observed from the experimental data plots, about 0.13 sec for the low wind speed, and about 1.08 sec for the high wind speed.  The reason for this difference can possibly be attributed to the noise in the wave gages.

Sources of Error:

As with any experiment, there are sources of error that tend to skew the data and throw off the results.  The sources of error that I have determined for my experiment are as follows:

1.   Repeatability of Experiment: 

Since I was limited to using only two wave gages, I had to perform the experiment multiple times in order to collect data at different distances from the fan.  It is difficult to precisely repeat experiments; therefore some of the error could be attributed to variability of the repeated experiments.

2.   Wave Gage Calibration: 

The wave gages must be properly calibrated prior to their use.  An error in the calibration process could skew all the data.

3.   Resolution of the Wave Gages: 

The manufacturer of the wave gages claims that they have a sensitivity of 0.1 mm.  Since the wave gages are fairly old, their sensitivity could have diminished which would result in less accurate data.

4.   Water Temperature: 

Since the water in the flume had been sitting idle for a long time before I conducted my experiment, the temperature of the water may not have been uniform which would mean the density is not uniform.  A lack of uniform water density could cause the wave generation to be uneven.

Validity of Theoretical Models: