Wave height increase from storm surge and surge protection

from barrier islands and coastal wetlands

CEE 514 – Coastal Engineering Final Project

By Nick Bennett

University of Wisconsin-Madison

Table of Contents

Introduction

Motivation

Background/Methodology

Analysis

Conclusion

References


Introduction

Hurricanes and tropical storms are very dangerous naturally occurring weather events.  Each year the United States coast is affected by these storms and the associated destruction that they create.  This includes damage due to high wind speeds and the subsequent storm surge and increased wave height that come along with it.  Flooding from this surge and the energy inherent in the storm cause even more damage.  While the damage caused by storms can be substantial in coastal areas, it would undoubtedly be greater if not for naturally occurring obstacles such as barrier islands and coastal wetlands.  I will analyze whether or not wave height is increased when there is storm surge, and the effect that barrier islands and wetlands have on dampening the storm's intensity.

Motivation

Growing up in the Southeastern United States I have a natural interest in tropical storms and hurricanes and why they create so much damage.  My goal is to understand how storms create so much damage from the surge they produce and how it could be worse without natural obstacles.

Background/Methodology

     
Storm Surge is the difference between the observed water level and the normal astronomical tide.  When storms with high wind push the water towards land, the water builds up and "surges" inland.  The increased depth of this water plays a crucial role in how wave height is affected at this point.                                                                                                     

Coastal Wetlands are primarily made up of tall grasses that impede the progress of waves moving through them.  If the grass is high enough it can affect the wave action and the      
energy that the wave has.  However when the grasses are completely covered with water it does little to affect the wave movement. 
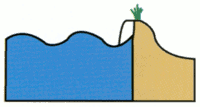
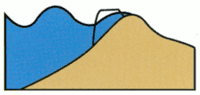
                  Grass              1 2  3 4                                                 Grass Wetlands (LaCoast)                           1.Regular water height            2.Storm surge slamming island      3.Storm surge overtaking island     4.Island inundated under surge

Barrier islands cause an obstacle to storm surge and diminish the energy of the storm.  Above is a depiction of the stages of storm surge overtaking a barrier island.  Sediment is transported as the waves eat away at the island, but the transport of the sediment takes great energy to accomplish this.  This will be energy that is not put to work damaging the mainland.

Analysis
First I need to state my assumptions for calculating the wave height due to increased storm surge.  I am assuming that the hurricane is a category 5 storm with wind speeds of 155mph, which is approximately 69.3 m/s.  I am also assuming that it is a 6 hour long storm in which the wind speed is unchanging.
                                                                                                                    

                                                                                                                                                                  

Saffir-Simpson Hurricane Scale

Category

Wind speed

Storm surge


mph
(km/h)

ft
(m)

5

≥156
(≥250)

>18 (>5.5)

4

131–155
(210–249)

13–18
(4.0–5.5)

3

111–130
(178–209)

9–12
(2.7–3.7)

2

96–110
(154–177)

6–8
(1.8–2.4)

1

74–95
(119–153)

4–5
(1.2–1.5)

Additional classifications

Tropical
storm

39–73
(63–117)

0–3
(0–0.9)

Tropical
depression

0–38
(0–62)

0
(0)

                                                                                                                                                  (Wikipedia)

For the first part of my analysis I have used Professor Chin Wu's excel program for modeling wave heights.  I have assumed a fetch of 200 km for the open ocean, and I have used different water depths corresponding to an increased storm surge to model what the wave height would be in different scenarios.  My results are shown in the table below.

 

Fetch

Wind speed (m/s)

depth (m)

Wave height (m)

200 km

69.3

1

1.12

 

 

2

1.76

 

 

3

2.3

 

 

4

2.77

 

 

5

3.21

 

 

6

3.61

 

 

7

3.99

 

 

8

4.36

 

 

9

4.7

 

 

10

5.03

 

 

15

6.51

 

 

20

7.74

 

 

25

8.75

 

 

30

9.59

 

 

40

10.87

 

 

50

11.78

                                                                                                      Increase in wave height with increase in water depth due to storm surge


                                                                                         




Using the JONSWAP method I can calculate the theoretical wave heights for this storm at different locations.  I am analyzing a case of wave height in the open ocean where the fetch is still 200 km like I stated before.  In the second case I will calculate the wave height in a bay area, between a barrier island and the mainland. I am assuming a fetch of 2 km for the area between the barrier island and the mainland.  I am also assuming that the wind is coming straight perpendicular to the barrier island and to the mainland.  I am also assuming that the waves are coming straight in perpendicularly to the shoreline to simplify my calculations.  Diffraction and reflection also play a part in how high the wave height would be in the bay area.  However I am assuming that the barrier island is infinitely long and that there is no diffraction or reflection of the waves.  Diffraction and reflection would undoubtedly have an effect on making the wave height higher, however I am positive that the wave height with these variables taken into consideration would still not be as great as the wave height in the open ocean. My analysis is shown below.

JONSWAP equations:                                                                                                                  

F*=gF/Ua2                                                                                                                                                                                                                       

t*=gt/Ua

F*eff=(t*/68.8) 3/2

H*s=gHs/U102=.0016(F*eff)0.5 for duration limited

H*s=gHs/U102=.0016(F*)0.5 for fetch limited



In open water, before the surge gets to the barrier island, calculate the wave height:
F*=9.81m/s^2*200000m/(69.3m/s)^2=408.5
t*=9.81*(21600 sec)/(69.3m/s)=3057.7
F*eff=(3057.7/68.8)^1.5=296.3
F*>F*eff so the wave height is duration limited.
H*s=gHs/U102=.0016(296.3)^.5

Hs=13.5 m


In the bay area between the barrier island and the mainland, the fetch is now 2 km
F*=9.81m/s^2*200m/(69.3m/s)^2=4.085
t*=9.81*(21600 sec)/(69.3m/s)=3057.7
 F*eff=(3057.7/68.8)^1.5=296.3
F*<F*eff so the wave height is fetch limited.
H*s=gHs/U102=.0016(4.085)^.5
Hs=1.58 m


To account for diffraction I needed to come up with a diffraction coefficient.  I know it will be small and diffraction will only occur on the ends of the very long islands.  I assume that the waves approach the end of the islands at a Θ=90o angle.  I will also assume that the angle Β=45o.  It is still a 2km distance from the barrier island to the mainland, so from trigonometry I can find r. L is still 224.6m from my calculation before. Then:

r= 2km/sin(45o)=2828.4m

r/L=2828.4m/224.6m=12.59
From the table for finding the diffraction coefficient based on values of Θ,Β, and r/L, then kD is:

kD =0.07~0.08


A diffraction coefficient this small means that when the incident waves reach the shore the wave height will be much less than it was.  The significant wave height will then be much smaller than the 13.5m that I had calculated for wave height in the open ocean.  Reflection would still play a part in making the diffracted waves higher after they bounce off of the mainland.

These results show that a barrier island would in effect lower the wave height because of the lower fetch involved before the waves hit the mainland while in the bay.  As stated before it is a simplified calculation that does not take into account the forces of diffraction or reflection.  However, my diffraction coefficient from above shows that it is a valid statement.

                                                                       Aireal Photo Aireal Photo     

                                                                        A large barrier island like St. George Island, FL is a great first defense against storm surge (St. George Island)                               

In addition I am also analyzing the wave energy for the different wave heights I calculated above.  The higher the wave height, the higher the wave energy should be.  My assumptions in this analysis include the density of water is 1000 kg/m^3 and the period of the waves is 12 sec.

E=Ek+Ep=ρgH2L/8

Assuming it is deepwater offshore,

L0=1.56T2

L0=1.56(12sec)2=224.6m

E=(1000kg/m3)*9.81m/s2*(13.5m)2*224.6m/8=50.19MJ


Now calculating the Energy in the bay, between the barrier island and the mainland, still assuming it is deepwater:

E=Ek+Ep=ρgH2L/8

Assuming it is deepwater in the bay,

L0=1.56T2

L0=1.56(12sec)2=224.6m

E=(1000kg/m3)*9.81m/s2*(1.58m)2*224.6m/8= 687.5KJ


If you assume it is shallow water in the bay, then the wavelength will be different and you will get a different energy calculation:

Using the dispersion relationship and assuming the depth is 3 meters:

L=(gT2/2π)*tanh(2πd/L)


I used the wave calculator found at the site, http://www.coastal.udel.edu/faculty/rad/wavetheory.html, and found that the wavelength is:
L=64.2m         Then:

E=(1000kg/m3)*9.81m/s2*(1.58m)2*64.2m/8= 196.5KJ


The energy of the wave in the bay is even smaller if you assume it is in shallow water with a depth of 3 meters.  This proves that the energy of the waves between the barrier island and the mainland is much less than the energy of the waves that are hitting the barrier island directly from the open ocean.


Next I need to analyze how the coastal wetlands might affect the storm surge and wave height.  It is my belief that as long as the wetlands are not completely covered in water, the friction they provide against the wave action will limit the energy that the waves are carrying.


Depending on the depth of water over the wetlands, some percentage of wave energy will be dissipated.  From my knowledge I would think that if water is completely covering the grasses, the friction it creates with the water would not do much to the energy of the wave.  It would dissipate somewhere between 0% and 100% based on how high the water is over the grasses.  On the other hand, I believe that if the grass is coming above the water then it will be able to dissipate 100% of the wave energy and decrease the potential for damage to the mainland.  No good studies have been done to completely justify my thinking, but there are reports that agree somewhat with my assumptions.



                                                                                                

                                                                                                               Coastal Wetlands of Louisiana (LaCoast)

Conclusion

Storm surge from major hurricanes and tropical storms causes great damage to America's coastline because of the increased wave height that comes with it and the flooding that occurs.  The best defense for humans against this destructive force is another of mother nature's creations; barrier islands and coastal wetlands.  I have proven herein that wave height and wave energy are dissipated by the presence of barrier islands along the United States coastline.  In theory I also believe that coastal wetlands play a big role in quelling storm surges and diminishing wave energy.  Despite all of this, we still cannot completely escape the wrath of mother nature because the extreme force of storms such as hurricanes cannot be completely stopped by anything.  While my analysis has many assumptions and is far from perfect in its theory, I believe that I have done a successful job in proving how wave heights increase with increased water depth.  However one major caveat in my analysis is that when storm surge occurs near to shore it is partially due to the shallower water as you get near land.  It is hard to determine whether increased storm surge then increases wave height or decreases wave height.  It is too complicated a question for me to get a clear answer to, because you would need to analyze the surge and wave height of individual cases to get a feeling for what happens in particular storms.  I still feel I have proved that wave height does increase with deeper water, and that is a good enough conclusion for what I have been trying to understand.


References

“Islands.” Gulf Islands National Seashore-Mississippi District. 1 June 2003. < http://www.nps.gov/archive/guis/extended/MIS/MNature/Islands.htm>.

“Saffir-Simpson Hurricane Scale.” Wikipedia. < http://en.wikipedia.org/wiki/Saffir-Simpson_Hurricane_Scale>.

“St. George Island.” < http://www.neilbranch.com/aireal.htm>.

“Storm Surge”. < http://chps.sam.usace.army.mil/ushesdata/Georgia/chapters/chapter02/0204chapter02-SURGE.html>.

 “University of Delaware Wave Calculator.” University of Delaware. < http://www.coastal.udel.edu/faculty/rad/wavetheory.html>.

“Web Quest: Louisiana Wetlands - An American Resource.”  LaCoast. < http://www.lacoast.gov/education/classroom/webquest.htm>.

“Wetlands Break Waves, Quell Surge, Coastal Landscape Battles Weather to Protect Mainland.” LaCoast. < http://www.lacoast.gov/WaterMarks/2006-03/2protectMainland/>.