A large storm was predicted to hit the shores of Bayfield County from Saturday, November 22nd, through Monday, November 24th.  Mike Swenson, a graduate student in the Department of Geological Engineering, and I, an undergraduate in the Department of Geological Engineering, traveled up to Bayfield County early Saturday morning to record the effects of this storm.  According to the NOAA website, we were expecting winds to reach over thirty miles per hour, producing wave heights up to fourteen feet.  The storm was not quite as strong as expected, but the following describes what we encountered.  After the storm we traveled back to Madison to analyze our data.  My goal was to measure the wave run-up, and to compare these observed values to the run-up predicted using the Hunt (1959) and Wilson (1989) methods. 

Two recordings at the N-6 site were taken, one during the storm conditions, on November 23rd, and the second (shown here) on November 24th, during intermediate conditions.  Each recording lasted one hour.  During the storm conditions, we were forced to endure the bitter winter storm.  Snow was blowing in from the lake, and would build up on the protective case on the camera.  This meant that during that hour, one of use would need to standby and wipe the focal area clean every few minutes.  We tried applying Rain-X to the focal area, but this didn't work all that well. 

While the camera was filming, and Mike was wiping the lens, I was assembling a measuring stick that would be used to provide a scale to measure the distance the wave traveled up shore.  This turned out to be quite a process, because the markings on the measuring stick were not large enough to see from the top of the bluff.  We used duct tape to signify five foot increments, and electrical tape to signify one foot increments.  These both proved hard to read, but were manageable.  To the left is a picture of me and the measuring stick at a different site.  We used another, similar method, to compare with the first method.  We took a five foot section of the measuring stick and taped it off at one foot increments.  These tapings were easier to read, but here errors could have occurred when the stick was flipped end-for-end from the toe to just in front of the mean water level.

One last thing we measured at the site was the beach slope.  This was done using an inclinometer.

To analyze the videos, a scale was needed to measure the distance each wave traveled.  This was done by taking a piece of Saran Wrap, and taping it over a television screen.  The video segments when the measuring stick was used were viewed, and the scale on the stick was transferred to the Saran Wrap with a marker.  This provided a scale for all the waves recorded.  The distance the waves traveled up shore were recorded every other ten minutes of each one-hour storm.  This provided a good estimate of the wave action during that hour.

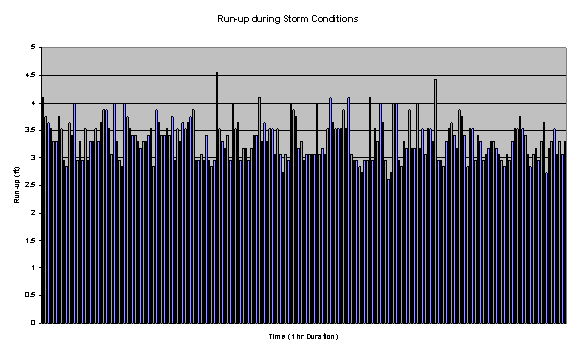
The distance the waves traveled were plotted over over the one-hour duration in which they took place.  Knowing the beach slope, α, these distances were then converted to run-up, which is the vertical distance traveled from the mean water level, and is shown below. 

Where:    Run-up = sin(α)*distance recorded

These were plotted during over the over a one hour interval as well, and can be seen below.

1)    Determining Significant Wave Height using JONSWAP method

In order to determine the predicted run-up,  the significant wave height is needed.  Given the fetch (the distance the wind travels across the water), F, the wind speed, U₁₀, and the duration of the wind, t_d, the significant wave height can be calculated using the JONSWAP (Joint North Sea Wave Project) method.

The first step is to determine if the storm is fetch limited or duration limited.  To do this, F^* and F_eff^* need to be calculated.

1)    F^* = gF/(U₁₀²)                                 where g = gravitational acceleration (32.2 ft/s)

and

2)    F_eff^* = (t^*/68.8)^1.5 where t^*= gt_d/U₁₀

If  F^* < F_eff^*, then the storm is fetch limited.  If F^* > F_eff^*, then the storm is duration limited.

The significant wave height, H_s, for a fetch limited storm is:

3)    H_s = ((U₁₀)²(0.0016)(F^*)^0.5)/g

The significant wave height, Hs, for a duration limited storm is:

4)    H_s = ((U₁₀)²(0.0016)(F_eff^*)^0.5)/g

2)    Classifying Wave-Break

Knowing the significant wave height, the surf similarity parameter, ξ_o, can be calculated to determine the breaker classification.

5)    ξ_o= (tan α)/((H_s/(L_o)^0.5)      where α is the slope of the beach, and L_o is the deepwater wavelength. 

L_o = 1.56T²                               where T is the wave period, determined by how much time it takes for one wave

                                                  to pass a given point, this value is recorded in meters, and needs to be converted.

The wave is a spilling breaker if:    ξ_o < 0.5

The wave is a plunging breaker if:    0.5 < ξ_o < 3.3

The wave is a surging breaker if:    ξ_o > 3.3

3)    Determining Run-up using Hunt (1959) and Walton (1989) method

Knowing the significant wave height, run-up, R, can now be determined.

If  0.1 < ξ_o < 2.3

6)    R = Hs*(tan α)/(Hs/Lo)^0.5

If ξ_o is large, then

7)    R = Hs*(sin α)/(Hs/Lo)^0.5

1)    Storm Conditions

During the storm, the winds were out of the northeast, blowing 30 miles per hour.  The fetch length determined was 250 miles, disregarding the effects of Isle Royale.  The winds were blowing in this direction at varying speeds for over 24 hours.  U₁₀ was chosen to be 20 miles per hour based on the variance of wind speed.  The time duration was chosen to be 24 hours, based on the data attained from the national weather service.

Given this, the storm was classified as duration limited, and the significant wave height, Hs, was found to be 9.67 feet.

Given the amount of waves that hit the shore during the hour, the period, T, was found to be 7 seconds.  This correlated to a deep-water wavelength of 250 feet.  Knowing the slope of the beach was 6.5 degrees, the surf similarity parameter was found to be 0.579.  These waves are classified as plunging.

Plugging the values for wavelength, Lo, slope, α, and significant wave height, Hs, into equation (7), the predicted run-up value could now be obtained. 

Predicted run-up, R, for the storm conditions was found to be 5.6 feet.

2)    Intermediate Conditions

The next day, November 24th, the winds had quieted, and shifted direction.  They were now blowing out of the northwest at 18 miles per hour.  The fetch length determined was 25 miles, and the duration of the northwest wind was 15 hours based on data obtained from the national weather service.

Given this, the winds were again classified as duration limited, and the significant wave height, Hs, was found to be 3.59 feet.

Given the amount of waves that hit the shore during the hour, the period, T, was found to be 4 seconds.  This correlated to a deep-water wavelength of 80 feet.  Knowing the slope of the beach was 6.5 degrees, the surf similarity parameter was found to be 0.538.  These waves are classified as plunging.

Plugging the values for wavelength, Lo, slope, α, and significant wave height, Hs, into equation (7), the predicted run-up value could now be obtained. 

Predicted run-up, R, for the intermediate conditions was found to be 1.9 feet.

Storm Predicted                                           Storm observed

Run-up:    5.6 ft                                            Average Run-up:    3.3 ft

The predicted run-up for the storm conditions was 2.3 feet greater than the observed run-up.  This may have been due to the predicted significant wave height.  The significant wave height was 9.67 feet, and may have marked the upper limit of the waves recorded during the storm.  From the videos, and observing the waves first hand, the largest waves may have reached heights close to ten feet, but many of them were much smaller.  The average wave height were probably much closer to six or seven feet.

Intermediate Predicted                                Intermediate Observed       

Run-up:    1.9 ft                                             Average Run-up:    2.0 ft

The predicted run-up for the intermediate conditions was very close to the observed run-up.  This leads one to believe that the prediction tools described above can provide accurate results.  The predicted significant wave height value, 3.59 feet, seems to be much closer to what was actually observed at the site.