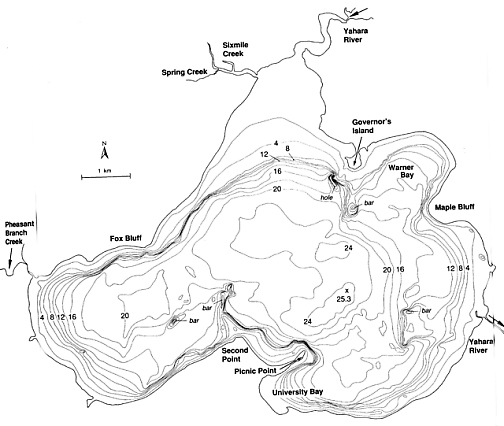
Physical
Model of Lake Mendota
The contour lines in this sketch are at 2 meter intervals
Froude number modeling will be used to relate the model to the prototype since gravitational forces are assumed to be more important that viscous ones.The equation for the Froude number is as follows:
![]()
Where u = velocity
g = gravity constant (9.81 m/s2)
L = length of any pertinent portion, usually the depth of the lake
To
keep the Froude number the same in the model and prototype the following
relationships will also be required.
| Characteristic | Dimension | Model to Prototype Scale Relation, r |
| Length | L | Lr = 1:9600 |
| Height | L | Lh = 1:120 |
| Area | L2 | Ar = Lr2 = 1:92160000 |
| Volume | L3 | Vr = Lr2Lh = 1:110,592,000,000 |
| Time | T | Tr = Lr1/2 = 97.98 |
| Velocity | L/T | vr = Lr /Lr1/2= 97.98 |
5. Model Construction
Using these dimensions, the model can then be constructed easily of plywood and plaster.The contours are being developed using the Madison Area Lakes map distributed by the Geological and Natural History Survey. Once drawn on a plywood base, they will be built up to the contours using drywall plaster with nails rising to the correct height as guides.Two different layers of this system will be required since the maximum nail height is 4 inches and the model will be roughly 8 inches high.
The sediment used to model that presently on the bottom of the lake will be selected in accordance with the Noda Model Law, which has been used successfully by the US Army Corp of Engineers in several model applications.
The sediment will be placed in a thin veneer on the model surface so that both scouring and filling can be examined.
Water cycling through the lake will be accomplished using a pump, which distributes water at the mouth of the Yahara and retrieves it at the Yahara Locks.
Wave action will be reproduces using motorized paddles and wind will be simulated with small, mechanized fans blowing from the prevailing wind direction.
As of this time, no mechanism will be used to model motorboat traffic since it is not considered a major sediment source.
Grace, P. J. (1989), Investigation of Breakwater Stability at Presque Isle Peninsula Erie, Pennsylvania, Technical Report CERC-89-3, Department of the Army, Buffalo, New York, pp 9-10.
Kamphius, J.W. (1985), “On Understanding Scale Effects in Coastal Mobile Bed Models,”Physical Modeling in Castal Engineering, (R.A. Dalrymple, Editor), A.A. Balkema, Rotterdam, pp. 141-162.
Murphy, G. (1950), Similitude in Engineering, The Ronald Press Company, New York, pp. 167-169.
Seabergh, W.C. (1983), Design for Prevention of Beach Erosion at Presque Isle Beaches, Erie, Pennsylvania, Technical Report HL-83-15, Department of the Army, Buffalo, New York, pp 9-20.
Wu,
C.H. (2000), Correspondence, University of Wisconsin-Madison.