A Review of Empirical and
Numerical Methods to Determine Wave Resistance on Ship Hull
ABSTRACT
MOTIVATIONS AND OBJECTIVES
There are two main motivations of this survey. The first is to gain a better understanding of hydrodynamics through the study of a practical problem that served to form the basis of fluid mechanics as it is traditionally regarded. The other motivation stems from the desire to develop a numerical protocol to evaluate hulls of concrete racing canoes. While many examples sited reference naval ships or other large sailing vessels, the same types of methods could be used to evaluate any sort of object in a flow field. If an accurate model can be developed that would save the money, time and energy that it costs to construct scale models of concrete canoes.
METHODS
In order to get a better understanding of how ship resistance has reached its current state. In the mid-late 1800, minimizing drag on a ship hull became a very important problem. Since most nations’ economies depended on ships to move goods between each other, fuel economy became important, as a ship business was limited to the distance it could travel without refueling with coal. The inevitable problem that arose was how to minimize drag with a very limited knowledge of the physics of drag reduction.
William Froude was a pioneer in the field of fluid mechanics and developed much of his legacy working on reducing hull drag. Froude was convinced that trial and error with these huge vessels represented an economically inefficient allocation of resources, convinced that scale model testing was a valuable method of testing ships before a prototype was created.
EFM
relation #1- Dimensional Analysis
Working with scale models requires the understanding of how that results can be scaled up to the prototype. Dimensionless numbers create a connection between parameters and develop functional relationship to correlate information in the small-scale tests.
For ship resistance, r,v,L,g,mall serve to influence a result, or:
![]()
Breaking the terms down into their Mass/Length/Time components and applying the Buckingham Pi Theorem, the three results become:
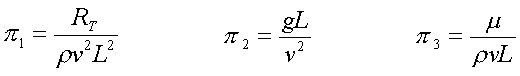
These values are all significant. The first represents the equation for dynamic drag of a fluid, while the second and third are the inverse of the Froude and Reynolds numbers respectively.
EFM relation #2- Dynamic Similitude
Part of the problem with scale models is making sure all the scaling variables are accounted for in the result. This requires geometric, kinematic and dynamic similitude.A well-constructed experiment can ensure geometric and kinematic similitude, but problems arise when trying to satisfy the third requirement. Evaluation of whether all the dimensionless parameters in the model match those of the prototype proves impossible because of the location of the velocity and length term in the two equations. In most applications, one of the parameters can be ignored due to the difference in magnitude, but in this case both wave and viscous forces contribute to the total drag, so neither can be ignored.
Froude found a way around this by breaking the resistance down, one component being a function of the Froude number and one being a function of the Reynolds number. The combination would yield a total coefficient of friction and introduce the idea of incomplete dynamic similitude in which experiments are run based on known values of the Froude number to determine total resistance. The Reynolds number kernel could be determined using the idea of equivalent flat plate resistance, and empirical method of determining surface resistance. The difference of the Froude component and the Reynolds component yield the wave resistance or energy loss as the body moves across the water surface.The basic steps are as follows:
We know that drag force depends only on Fr. Model speed can be estimated knowing:
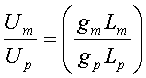
Using the Moody diagram, a Coefficient of Drag (CD) can be determined for both the model and the prototype. Skin Drag on the model can now be calculated:
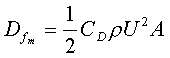
If total drag on the model is measured in a flume, the difference between Dtotal and Dskin is the wave resistance Dwave. Scale to Prototype:
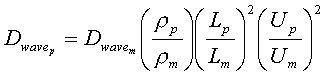
The friction drag can also be obtained with prototype values exactly as the model was.
A follow-up technique (should you have the luxury to have connections with the U.S. Navy) is an extrapolation method discussed in Ferguson. He contends that a relationship can be developed to link the sinkage and trim of a large ship to the sip resistance based on model test that very the Froude number. The results were then extrapolated to larger scale models and plotted against real data form those models.
Part 2 Numerical Models
EFM relation #3- Governing Equations and Boundary
Conditions
Even the best experiment still takes time and money to construct and run. As computers become more powerful and the knowledge base of computational fluid dynamics continues to grow, scientist and mathematicians have begun to search for new ways to evaluate hulls with computer modeling. A code that could determine the optimal hull design for applied conditions would be an invaluable resource for designers as it would eliminate any need for model testing.
There is a reason that this perfect code does not yet exist. The complicated mathematics coupled with various model assumptions has made reliable solutions more elusive than would be expected. The following will show some of the techniques used to solve this complicated problem using the basic governing equations of fluid mechanics.
One example (Sorti et al.) shows how conservation of momentum can be used in the calculation of wave resistance. Using a Laplacian governing equation, flow is assumed to be irrotational and incompressible and that Bernoulli’s equation applies at the free surface waves created in the control volume are assumed to pass through with the “absorbing boundary” that eliminates the viscous effects and allowing energy to leave the system and validating the momentum flux assumption.
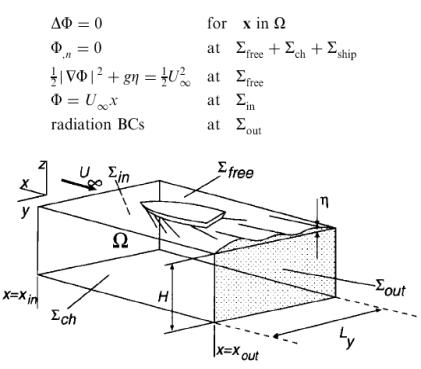
(From Sorti et al.)
If these conditions are met, a simple momentum balance at the plane ahead of the ship and behind the ship will produce a net decrease in flux equal to the wave-making resistance. Using the Bernoulli assumption, the description for momentum of a vertical plane of water before hitting the hull can be described as:
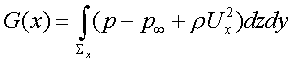
Once the water passes the body a perturbation technique to linearized to:
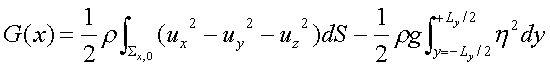
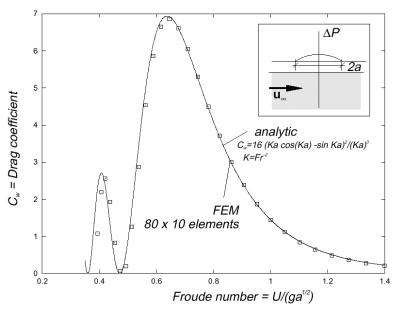
A finite element analysis uses this information to evaluate drag coefficients at different Froude numbers and outputs results like:
Idelson et al. also uses a finite element approach, but develops the solution a step further by using for Euler and Navier-Stokes Flow as a free surface boundary. The code predicts a velocity field and uses that information in a mass conservation to calculate a pressure field (using a Poisson Equation). The pressures obtained are then updated in the program and a new iteration is calculated. Like the previous technique, an equation is included to incorporate a radiation condition so as to eliminate any reflected energy that might occur in the artificial flow field. Some results of the analysis look like:

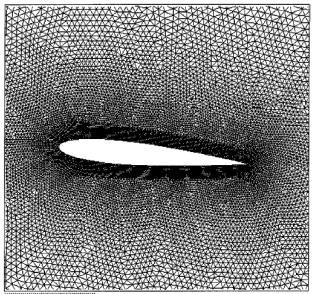
Meshes for 1. the Euler Equation, the Navier-Stokes
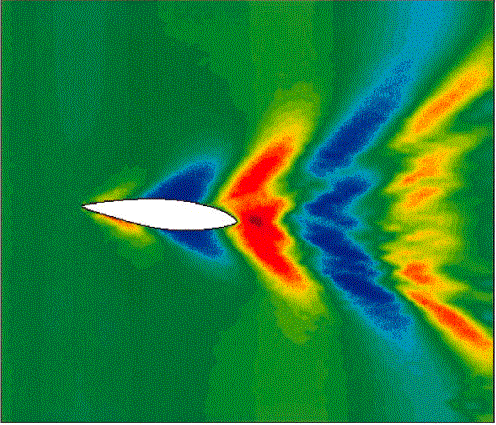
Results of wave pattern behind a
sailboat (Idelson).
DISCUSSION
The methods that have been described in this brief survey have all provided an application to all the note that were take in CEE 618 this year. The process of solving problems by first identifying variables, choosing governing equations and making simplifying assumptions, setting boundary conditions and the applying them to the to the governing equations to solve an eventual outcome, can bee seen in each reference listed.
As for the practicality of this author developing a code that will be helpful for evaluating a canoe hull, it may take a bit more research and training. Hopefully the reader has gained some appreciation of what goes into the process and how complicated it can actually become.
REFERENCES
Bessho, M.(1994). On a Consistent Linearized Theory of the Wave-Making Resistance
of Ships. Journal of Ship Research, Vol.38, No.2, pp. 83-96.
Chen, C.Y. and Noblesse, F. (1983) Comparison Between Theoretical Predictions of
Wave Resistance and Experimental Data for the Wigley Hull. Journal of Ship Research, Vol. 27, No.4, pp. 215-228
Ferguson, A.M. (1984) Extrapolation Method from Ship Resistance Based on the
Variation of Sinkage and Trim with Froude Number. Naval Architect, January 1984, pp. 17-32
Gillmer, T.C. and Johnson, B (1982) Introduction to Naval Architecture. Naval Institute
Press, Annapolis, Maryland
Idelsohn, S.R. , Onate, E. and Sacco, C. (1999) Finite Element Solution of Free-Surface
Ship-Wave Problems, International Journal for Numerical Methods in Engineering, No. 45, pp. 503-528
Kostyukov, A.A.(1968) Theory of Ship Waves and Wave Resistance, E.C.I., Iowa City,
Iowa
Kundu, P.J. (1990) Fluid Mechanics, Academic Press, San Diego, California
Larsson, L. and Baba, E. (1996) Ship
Resistance and Flow Computations. Advances in
Marine Hydrodynamics, Vol. 5, pp 1-75, Computational Mechanics Publications, Southampton, Boston
Roberson, J.A. and Crowe, C.T. (1997) Engineering Fluid Mechanics, John Wiley &
Sons, Inc., New York, New York
Storti, M. , D'elia, J. and Idelsohn, S. (1998) Computing Ship Wave Resistance from
Wave Amplitude
with Non-local Absorbing Boundary Condition. Communications
in Numerical Method
of
Engineering, no. 14, pp. 997-1012.